If you work with databases you are probably familiar with B-Tree indexes. They are used to enforce unique and primary-key constraints, and are the default index type in most database engines. If you work with text, geography or other complex types in PostgreSQL, you may have dipped your toes into GIN or GIST indexes. If you manage a read intensive database (or just follow this blog), you may also be familiar with BRIN indexes.
There is another type of index you are probably not using, and may have never even heard of. It is wildly unpopular, and until a few PostgreSQL versions ago it was highly discouraged and borderline unusable, but under some circumstances it can out-perform even a B-Tree index.
In this article we re-introduce the Hash index in PostgreSQL!
This article was co-authored by Michael from pgMustard

Table of Contents
Hash Index
Just like the name suggests, Hash indexes in PostgreSQL use a form of the hash table data structure. Hash table is a common data structure in many programming languages. For example, a Dict in Python, a HashMap in Java or the new Map type in JavaScript.
To understand how you can benefit from Hash indexes, it's best to understand how they work.
Hash Function
Hash indexes use a hash function. PostgreSQL's hash function maps any database value to a 32-bit integer, the hash code (about 4 billion possible hash codes). A good hash function can be computed quickly and "jumbles" the input uniformly across its entire range.
The hash codes are divided to a limited number of buckets. The buckets map the hash codes to the actual table rows.
A simple hash function for an integer type is modulo: divide a number by another number, and the remainder is the hash code. For example, to divide values across 3 buckets you can use the hash function mod(3):
db=# SELECT n, mod(n, 3) AS bucket FROM generate_series(1, 10) AS n;
n │ bucket
────┼────────
1 │ 1
2 │ 2
3 │ 0
4 │ 1
5 │ 2
6 │ 0
7 │ 1
8 │ 2
9 │ 0
10 │ 1
When a new value is added to the index, PostgreSQL applies the hash function to the value and puts the hash code and a pointer to the tuple in the appropriate bucket. In the example above using the hash function mod(3), if you insert the value 5 the index entry will be added to bucket 2, because 5 % 3 = 2.
When you query a value using a Hash index, PostgreSQL does the opposite. It takes the value and applies the hash function to determine which bucket may hold matching tuples. Once the bucket is identified, PostgreSQL will fetch the tuples referenced in that bucket and match them against your query.
Hash Collision
You may have noticed that multiple values can map to the same bucket; this is called a collision. For example, the hash function mod(3) returned the hash code 2 for the values 2, 5 and 8.
What PostgreSQL actually does, is to first use a hash function to produce an integer hash code:
db=# SELECT
hashtext('text'),
hashchar('c'),
hash_array(array[1,2,3]),
jsonb_hash('{"me": "haki"}'::jsonb),
timestamp_hash(now()::timestamp);
─[ RECORD 1 ]──┬────────────
hashtext │ -451854347
hashchar │ 203891234
hash_array │ -325393530
jsonb_hash │ -1784498999
timestamp_hash │ 1082344883
It then uses mod(n_buckets) to determine which bucket the tuple should be put in. This can cause multiple values to end up in the same bucket. This is why even after the bucket is identified, the database still needs to sift through the hash codes in the bucket and recheck the condition to filter only the matching tuples.
As rows are added to the index, it's possible for a bucket's primary page to fill up. In this case, additional rows are written to overflow pages. The overflow pages contain index entries that did not fit in the bucket's primary page.
Index Split
At some point, the database can decide it needs to split a bucket into two buckets. PostgreSQL uses special hash functions that ensure values in a bucket can be split into exactly two buckets. When a bucket is split, additional storage is allocated to the index.
Luckily, PostgreSQL does all the heavy lifting for you, so you don't have to decide what hash function to use, or how many buckets there are.
If you want to learn more about the internals of Hash indexes in PostgreSQL, check out the readme on "Hash Indexing".
Hash Index in PostgreSQL
Hash indexes were discouraged prior to PostgreSQL 10. If you read the index type documentation for PostgreSQL 9.6 you'll find a nasty warning about Hash indexes. According to the warning, Hash indexes are not written to the WAL so they cannot be maintained in replicas, and they are not automatically available after a crash, so you need to manually rebuild them.
Starting at PostgreSQL 10 these limitations were resolved, and Hash indexes are no longer discouraged.
Creating Hash Indexes
Now that you know how Hash indexes work in PostgreSQL, you are ready to see them in action. To illustrate, we'll create an imaginary URL shortening service.
A URL shortener service, such as "bit.ly" or the late "goo.gl", provides a short random URL that points to a longer URL. For example, you can have the short url https://short.url/hb9837 point to the longer URL https://hakibenita.com/automating-the-boring-stuff-in-django-using-the-check-framework. We'll call the hb9837 part of the short URL the key.
To implement your URL shortening service, create a table to store the mapping between the keys and the full URLs:
CREATE TABLE shorturl (
id serial primary key,
key text not null,
url text not null
);
The table includes an auto incrementing primary key id, a text field for key, and a url field containing the full URL.
Next, create a B-Tree and a Hash index on both fields:
CREATE INDEX shorturl_key_hash_index ON shorturl USING hash(key);
CREATE UNIQUE INDEX shorturl_key_btree_index ON shorturl USING btree(key);
CREATE INDEX shorturl_url_hash_index ON shorturl USING hash(url);
CREATE INDEX shorturl_url_btree_index ON shorturl USING btree(url);
You might have noticed that the B-Tree on key is a unique index, but the Hash index is not. This is because Hash indexes currently cannot be used to enforce unique constraints.
Hash Index Size
The first thing you want to do is to compare the size of a Hash index to the size of a similar B-Tree index:
CREATE EXTENSION "uuid-ossp";
DO $$
BEGIN
FOR i IN 0..1000000 loop
INSERT INTO shorturl (key, url) VALUES (
uuid_generate_v4(),
'https://www.supercool-url.com/' || round(random() * 10 ^ 6)::text
);
if mod(i, 10000) = 0 THEN
RAISE NOTICE 'rows:% Hash key% B-Tree key:% Hash url:% B-Tree url:%',
to_char(i, '9999999999'),
to_char(pg_relation_size('shorturl_key_hash_index'), '99999999999'),
to_char(pg_relation_size('shorturl_key_btree_index'), '99999999999'),
to_char(pg_relation_size('shorturl_url_hash_index'), '99999999999'),
to_char(pg_relation_size('shorturl_url_btree_index'), '99999999999');
END IF;
END LOOP;
END;
$$;
To get a better sense of how both indexes behave, keep track of the size of the indexes as rows are inserted to the table:
- Generate 1,000,000 short urls one by one
- Every 10,000 rows log the size of all four indexes
- Use
uuid_generate_v4from the uuid-ossp package to generate UUIDs as keys - Generate a long URL from a 6-digit domain so it's not unique, but almost unique
Running the script on PostgreSQL 13 and plotting the results gives the following chart:
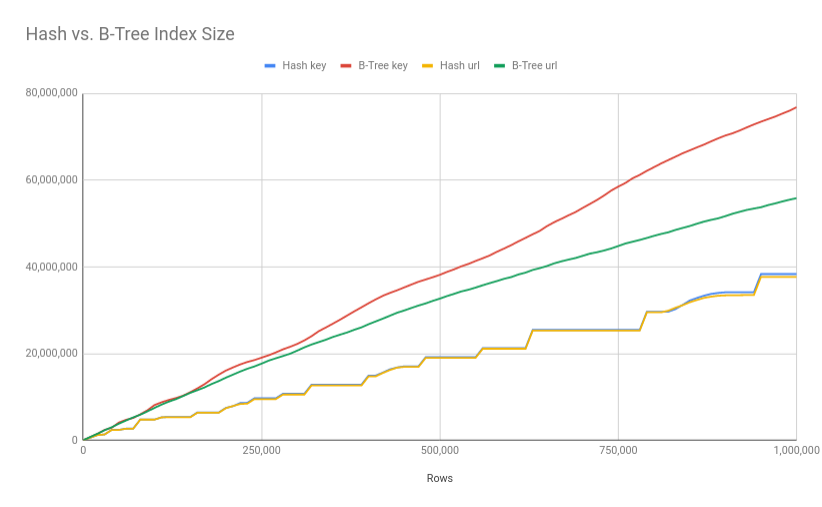
The chart provides several interesting observations:
-
The Hash index is smaller than the B-Tree index: Almost all along the way, the Hash index on both fields is smaller than the size of the corresponding B-Tree index.
-
Hash index grows in increments: Unlike the B-Tree index that seems to grow linearlly as rows are inserted to the table, the Hash index grows in sudden increments. These sudden increments are caused when a split is triggered to allocate space for more buckets. When that space runs out, another split is triggered and so on.
-
Hash index size is not affected by the size of the indexed value: A Hash index stores the hash codes of the index field values. A B-Tree on the other hand, stores the actual value of the indexed field in its leaves, so the size of the indexed value affects the size of a B-Tree index, but not the size of a Hash index.
-
Hash index size is not affected by the selectivity of the indexed value: The selectivity of the URL field is different than that of the key field, which is almost unique, but the Hash index on both fields is the same size. A size of a B-Tree index on the other hand, can vary based on the selectivity of the data (see note below about "B-Tree deduplication").
B-Tree deduplication
PostgreSQL 13 introduced a new B-Tree deduplication mechanism that reduces the size of a B-Tree indexes with many duplicate values. In the chart above, the size of the B-Tree index on the url field is smaller than the size of the index on the key field because it has fewer unique values.
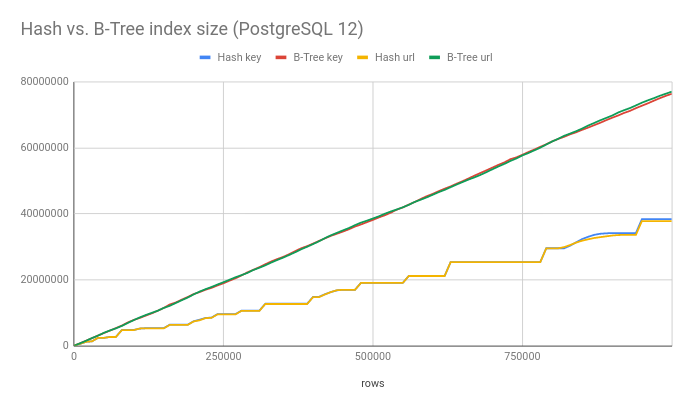
If you run the same script with deduplication disabled, or on PostgreSQL versions prior to 13, you'll see that the size of the index is the same (as long as values are the same size).
The script you ran before imitates a workload of an OLTP-like system, where single rows are constantly being added to the table. This is the size of the indexes after the script finished:
db=# \di+ shorturl*
Name │ Type │ Table │Size
─────────────────────────┼───────┼──────────┼────────
shorturl_key_btree_index │ index │ shorturl │ 73 MB
shorturl_key_hash_index │ index │ shorturl │ 37 MB
shorturl_url_btree_index │ index │ shorturl │ 53 MB
shorturl_url_hash_index │ index │ shorturl │ 36 MB
At this point the Hash indexes are roughly half the size of the corresponding B-Tree indexes. To make an even more strict comparison, reindex the table and let the DB rebuild the indexes from scratch:
db=# REINDEX TABLE shorturl;
REINDEX
db=# \di+ shorturl*
Name │ Type │ Table │ Size
─────────────────────────┼───────┼──────────┼───────
shorturl_key_btree_index │ index │ shorturl │ 56 MB
shorturl_key_hash_index │ index │ shorturl │ 32 MB
shorturl_url_btree_index │ index │ shorturl │ 41 MB
shorturl_url_hash_index │ index │ shorturl │ 32 MB
Reindexing reduced the size of all the indexes, some more than others. Reindexed, both Hash indexes are still smaller than the corresponding B-Tree indexes.
Hash Index fillfactor
A useful storage parameter that affects when a Hash index is split is fillfactor. In a Hash index, the fillfactor parameter controls the ratio between tuples and buckets that triggers a split. The lower the fillfactor, the more "empty" space in the index.
The default fillfactor for a B-Tree index is 90, for a Hash index the default is 75. To illustrate how fillfactor affects the size of a Hash index, compare the size of Hash indexes with different fillfactor while inserting rows into the table:
CREATE TABLE shorturl_ff (
id serial primary key,
key text not null,
url text not null
);
CREATE INDEX shorturl_key_hash_index_025 ON shorturl_ff USING hash(key) WITH (fillfactor = 25);
CREATE INDEX shorturl_key_hash_index_050 ON shorturl_ff USING hash(key) WITH (fillfactor = 50);
CREATE INDEX shorturl_key_hash_index_075 ON shorturl_ff USING hash(key) WITH (fillfactor = 75);
CREATE INDEX shorturl_key_hash_index_100 ON shorturl_ff USING hash(key) WITH (fillfactor = 100);
DO $$
BEGIN
RAISE NOTICE 'rows,25,50,75,100';
FOR i IN 0..1000000 LOOP
INSERT INTO shorturl_ff (key, url) VALUES (
uuid_generate_v4(),
'https://www.supercool-url.com/' || round(random() * 10 ^ 6)::text
);
IF mod(i, 10000) = 0 THEN
RAISE NOTICE '%,%,%,%,%',
to_char(i, '9999999999'),
pg_relation_size('shorturl_key_hash_index_025'),
pg_relation_size('shorturl_key_hash_index_050'),
pg_relation_size('shorturl_key_hash_index_075'),
pg_relation_size('shorturl_key_hash_index_100');
END IF;
END LOOP;
END;
$$;
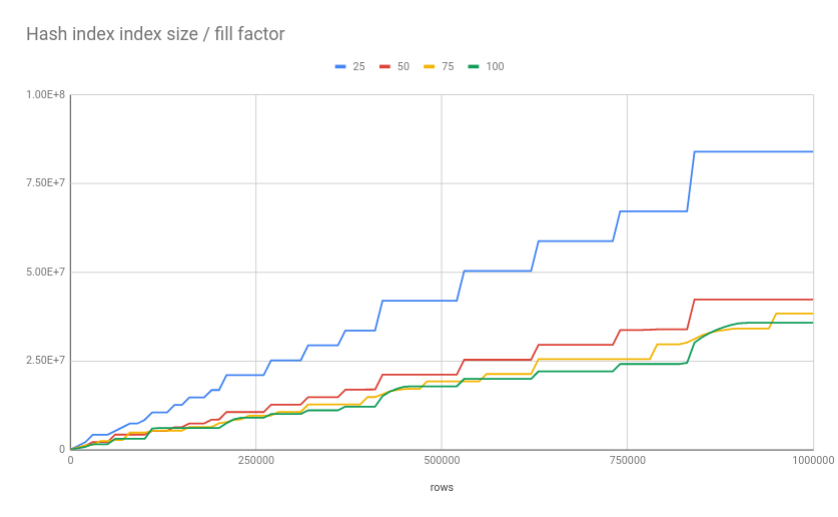
The chart confirms that low fillfactor values trigger bucket splits sooner, which leads to a larger index size. Unlike B-Tree indexes that reserve space for updated rows, new values in a Hash index can go to any bucket, so keep that in mind when you adjust the fillfactor for a Hash index.
Hash Index Performance
Striking a good balance between index size and speed is key to a healthy database. So far you've seen that Hash indexes can be smaller in size than similar B-Tree indexes under some circumstances, but can a Hash index be faster than a B-Tree?
Hash Index Insert Performance
When you insert a row into a table, the row is also inserted into all the indexes on the table. Having many indexes on a table can speed up queries, but it might have the opposite effect on inserts.
To determine the effect of Hash indexes on insert performance, create the shorturl table, and add a Hash index on the key column:
DROP TABLE IF EXISTS shorturl_hash;
CREATE TABLE shorturl_hash (
id serial primary key,
key text not null,
url text not null
);
CREATE INDEX shorturl_hash_hash_ix ON shorturl_hash USING hash(key);
Next, insert 1M rows one by one, and get the total and average timing:
DO $$
DECLARE
n INTEGER := 1000000;
duration INTERVAL := 0;
start TIMESTAMP;
uid TEXT;
url TEXT;
BEGIN
FOR i IN 1..n LOOP
uid := uuid_generate_v4()::text;
url := 'https://www.supercool-url.com/' || round(random() * 10 ^ 6)::text;
start := clock_timestamp();
INSERT INTO shorturl_hash (key, url) VALUES (uid, url);
duration := duration + (clock_timestamp() - start);
END LOOP;
RAISE NOTICE 'Hash: total=% mean=%', duration, extract('epoch' from duration) / n;
END;
$$;
Hash: total=00:00:09.764746 mean=9.764746e-06
Inserting 1M rows one by one into a table with a Hash index took just under 10s.
Executing the same script on a table with a B-Tree index produces the following results:
DROP TABLE IF EXISTS shorturl_btree;
CREATE TABLE shorturl_btree (
id serial primary key,
key text not null,
url text not null
);
CREATE INDEX shorturl_btree_hash_ix ON shorturl_btree(key);
DO $$
DECLARE
n INTEGER := 1000000;
duration INTERVAL := 0;
start TIMESTAMP;
uid TEXT;
url TEXT;
BEGIN
FOR i IN 1..n LOOP
uid := uuid_generate_v4()::text;
url := 'https://www.supercool-url.com/' || round(random() * 10 ^ 6)::text;
start := clock_timestamp();
INSERT INTO shorturl_btree (key, url) VALUES (uid, url);
duration := duration + (clock_timestamp() - start);
END LOOP;
RAISE NOTICE 'B-Tree: total=% mean=%', duration, extract('epoch' from duration) / n;
END;
$$;
B-Tree: total=00:00:10.822158 mean=1.0822158e-05
Inserting 1M rows one by one to a table with a B-Tree index took almost 11s. While far from scientific, this test shows that a Hash index has less impact on insert performance than a B-Tree index.
Hash Index Select Performance
In your URL shortening service, you want to be able to quickly look up a URL based on its key. To see how a Hash index performs in relation to a B-Tree, run a benchmark to query the table many times using the index, and get the total and average timing:
DO $$
DECLARE
n INTEGER := 100000;
duration INTERVAL := 0;
start TIMESTAMP;
keys TEXT[];
BEGIN
-- Fetch radom keys from the table
SELECT ARRAY_AGG(key) INTO keys
FROM (
SELECT key
FROM shorturl_hash
ORDER BY random()
LIMIT n
) AS foo;
FOR i IN array_lower(keys, 1)..array_upper(keys, 1) LOOP
start := clock_timestamp();
PERFORM * FROM shorturl_hash WHERE key = keys[i];
duration := duration + (clock_timestamp() - start);
END LOOP;
RAISE NOTICE 'Hash: total=% mean=%', duration, extract('epoch' from duration) / n;
END;
$$;
Hash: total=00:00:00.590032 mean=5.90032e-06
Selecting 100K random keys from the table one by one took just over half a second.
Next, execute the same on a table with a B-Tree index:
Code
DO $$
DECLARE
n INTEGER := 100000;
duration INTERVAL := 0;
start TIMESTAMP;
keys TEXT[];
BEGIN
-- Fetch radom keys from the table
SELECT ARRAY_AGG(key) INTO keys
FROM (
SELECT key
FROM shorturl_btree
ORDER BY random()
LIMIT n
) AS foo;
FOR i IN array_lower(keys, 1)..array_upper(keys, 1) LOOP
start := clock_timestamp();
PERFORM * FROM shorturl_btree WHERE key = keys[i];
duration := duration + (clock_timestamp() - start);
END LOOP;
RAISE NOTICE 'B-Tree: total=% mean=%', duration, extract('epoch' from duration) / n;
END;
$$;
B-Tree: total=00:00:00.923244 mean=9.23244e-06
While both are fast, you can see that Hash index outperforms the B-Tree index with a very slight difference.
Hash Index Limitations
Hash index benefits do not come without a cost. While it can outperform a B-Tree under some circumstances, it has many limitations.
Hash index cannot be used to enforce a unique constraint:
db=# CREATE UNIQUE INDEX shorturl_unique_key ON shorturl USING hash(key);
ERROR: access method "hash" does not support unique indexes
Hash index cannot be used to create indexes on multiple columns:
db=# CREATE INDEX shorturl_key_and_url ON shorturl USING hash(key, url);
ERROR: access method "hash" does not support multicolumn indexes
Hash index cannot be used to create sorted indexes:
db=# CREATE INDEX shorturl_sorted_key ON shorturl USING hash(key desc);
ERROR: access method "hash" does not support ASC/DESC options
If you don't mind these limitations and you decided to create a Hash index, there are some limitations on using Hash indexes as well.
You can't use a Hash index to cluster a table:
db=# CLUSTER shorturl USING shorturl_url_hash_index;
ERROR: cannot cluster on index "shorturl_url_hash_index" because access method does not support clustering
Clustering
Not sure what the CLUSTER command does? or why you would want to use it? Check out my tip on always loading sorted data into tables.
Hash index cannot be used for range lookups:
db=# EXPLAIN (COSTS OFF) SELECT * FROM shorturl WHERE key BETWEEN '1' AND '2';
QUERY PLAN
────────────────────────────────────────────────────────────────────────────────
Gather
-> Seq Scan on shorturl
Filter: ((key >= '1'::text) AND (key <= '2'::text))
A Hash index cannot be used to satisfy ORDER BY queries:
db=# EXPLAIN (COSTS OFF) SELECT * FROM shorturl ORDER BY key LIMIT 10;
QUERY PLAN
────────────────────────────────────────────────────────────────────────────────
Limit
-> Index Scan using shorturl_key_btree_index on shorturl
The database is able to use the B-Tree index on the key field to satisfy the query, but not the Hash index. To make sure, drop the B-Tree and check again:
db=# BEGIN;
BEGIN
db=# DROP INDEX shorturl_key_btree_index;
DROP INDEX
db=# EXPLAIN (COSTS OFF) SELECT * FROM shorturl ORDER BY key LIMIT 10;
QUERY PLAN
─────────────────────────────────────────────────
Limit
-> Gather Merge
Workers Planned: 2
-> Sort
Sort Key: key
-> Parallel Seq Scan on shorturl
(6 rows)
db=# rollback;
ROLLBACK
Even without the B-Tree the Hash index is not being used.
invisible indexes
Generating a query execution plan with the absence of an existing index without actually dropping it is extremely useful. Check out my tip on "Invisible Indexes".
Conclusion
Hash maps are usually the go-to data structure for storing data for fast retrieval by key. However, in the main data store, the database, we rarely use this data structure. In PostgreSQL at least, this is most likely because the implementation prior to version 10 was very restrictive, and DBAs and developers just got used to dismissing it.
This is a quick recap of our re-introduction to Hash indexes in PostgreSQL:
- Hash index is usually smaller than a corresponding B-Tree index
- Hash index select and insert performance can be better than a B-Tree index
- Hash index removed many of its restrictions in PostgreSQL 10, and is now safe to use
- Hash index has many restrictions that limit its use to very specific use cases
If you are interested in the internals of a Hash index, don't miss the readme in the source.
